Biophysical Chemistry Textbook (Work in Progress)

by John Della Rosa

Protein Folding Biophysics

Introduction

Prerequisites

This chapter will not contain much math. However, an understanding of optimization will be useful.
Some basic thermodynamics knowledge will be assumed. You should understand the basics of:
- What entropy and enthalpy are, at least at a conceptual level
- The various types of intermolecular and intramolecular forces
Basic organic chemistry knowledge will be assumed. You should be familiar with the following:
- Common functional group names and structures
- Conjugation/Resonance

Thermodynamics of Protein Folding

Enthalpy and Entropy

The concepts of enthalpy and entropy will be focused on in this chapter. If you are uncomfortable with them, then you should read the earlier chapters on thermodynamics.

What is the primary driver of protein folding? It is the hydrophobic effect. The hydrophobic effect is where the hydrophobic parts of the protein are burried together away from water and only the hydrophilic parts of the protein are exposed. When the hydrophobic parts of the protein are burried, water molecules are freed from having to form an ordered shell. This allows for more hydrogen bonding, but even moreso, an increase in entropy for the water excluded.

Protein Folding Structures

Primary Structure

The primary structure of a protein is the sequence of amino acids, connected by amide linkages between the carboxylate group of the earlier one in the sequence and the amine group of the following one.

Secondary Structure

The secondary structure involves hydrogen bonding between amide backbones of residues. There are two main conformations that the protein can fold itself into to do this.

Alpha helix
Beta sheet

There are a few other secondary structures that occur, but they are so rare that they are not worth mentioning. A single protein can have many instances of both alpha helices and beta sheets in it.

Phi, Psi, and Omega Angles

When talking about conformations that the peptides are in, it becomes useful to consider 3 different bonds and the dihedral angles along them.

Omega: the peptide bond
Phi: the bond between the alpha carbon and the nitrogen
Psi: the bond between the alpha carbon and the carbonyl carbon

By Dcrjsr, vectorised Adam Rędzikowski - Own work, CC BY 3.0, Link

Ramachandran Diagram

By Dcrjsr - Own work, CC BY 3.0, Link

In order for a secondary structure to form, the phi and psi angles of a series of consecutive residues must fall within certain regions. For the right-handed alpha helix and beta sheets, phi is negative. The left-handed alpah helix is much rarer and is one of the few instances of having consecutive positive phi values.

Omega is left out from the diagram as it is heavily restricted to either 0 or 180 degrees. This is in order to maintain conjugation of the pi system between the oxygen, carbon, and nitrogen of the amide. Furthermore, omega has a strong preference for being at 180 degrees (trans, where the two alpha carbons are catty-corner) due to steric clashes between the two alpha carbons being on the same side of the C=N bond (cis). Proline can be an exception when it is directly after the amide bond due to its ring.

Alpha Helix

The alpha helix involves the backbone carbonyl oxygen of residue i hydrogen bonding with the hydrogen attached to the nitrogen of the amide of residue i+4. When viewed from above, the angle between the i'th residue, the center axis, and the i+1'th residue is approximately 100 degrees.

Since all the hydrogen bonds in the helix share the same orientation, the alpha helix has an overall dipole, called the macro-dipole. The overall dipole is positive at the N-terminal side and negative at the C-terminal side. In cartoon depictions, alpah helices are shown as cylinders or a single helix.

Beta sheets

Beta sheets also involve backbone hydrogen bonding between amides, but the hydrogen bonded pairs are not as close in the sequence. The basic unit of a beta sheet is the beta strand. In a beta strand, there is a 180 angle difference between consecutive residues. If one were to imagine a plane on which the beta strand lied, the carbonyl oxygen would be alternatingly pointing up and down with each residue. A similarly geometry is present for the side chain positioning. Thus, a beta strand does not hydrogen bond with itself. Another beta strand will be positioned above such that the plane for that strand is roughly parallel. Plane 1's upward facing nitrogens and carbonyl will hydrogen bond with plane 2's downward facing carbonyl and nitrogen respectively. In reality, there is some curvature in the beta strand. More than two beta strands can be present as each plane still has another available side in this scenario.

Another consideration for beta-sheets is whether the pairing is parallel or anti-parallel. This refers to if the N-terminal ends of the strands are aligned or oppositely aligned in space. Both are possible and there can be a mixture within a single beta sheet.

In cartoon depictions, beta strands are arrows, where the arrow head points from n-terminus to the c-terminus.

Collagen helix

The collagen helix is another possible secondary structure which appears as a triple helix. As the name suggests, it is present in types of collagen.

Motifs

Combinations of beta strands/sheets and/or alpha helices are often observed in proteins 3D structures. Common patterns are called motifs.

Tertiary Structure

The tertiary structure involves further folding of the protein onto itself with various forms of interaction.

Covalent bonds (Cysteine-Cysteine disulfide bridge)
Ionic bonds
Polar bonds
Van der Waals force

Quartenary Structure

Multiple tertiary structures can come together to form a quarternary structure

Protein Folding Models

Anfinsen's Thermodynamic Hypothesis

The thermodynamic hypothesis states that the native structure of a protein is determined just by its sequence. It may be surprising that all the thermodynamic directions for complicated folding are encoded in the sequence. This requires stability, uniqueness, and kinetic accessibility. In general, this holds well, although notable counterexamples exist for each requirement.

Levinthal's Paradox

We saw that each residue had phi, psi, and omega angles that have energetically preferred values. And in a protein, there can easily be over a hundred residues, who can interact with each other. Given how many parameters there are to optimize, how are proteins able to fold as quickly as they do? Anfinsen's thermodynamic hypothesis states that for a lot of proteins, the primary structure is sufficient to yield a unique 3D structure without outside assistance. This is essentially Levinthal's paradox, that proteins are observed to be able to fold at a much faster speed than they would through random sampling of possible confirmations.

Hierarchical Folding

Hierarchical folding model attempts ot address part of Levinthal's paradox by stating that the search space is narrowed down significantly by proteins first folding into secondary structures and then tertiary structures. A related concept is the hydrophobic collapse process.

Difficult Problem in Optimization

One of the biggest, if not the biggest, issues in optimization is local minima. It is (relatively) simple to always go downhill to find the minimizer of a function, but what if there exists local minimizers in addition to the global minimizer.

Example

In the below example, we have an optimization problem with two minima. Say we are at the point x=-3, we can go downhill to the right and find a minimum around \(x\approx -2\). However, this is not the global minimum. In order to then get to the global minimum, we would have to go uphill again to the right. There is not real way for our algorithm to know that there exists a lower point somewhere else.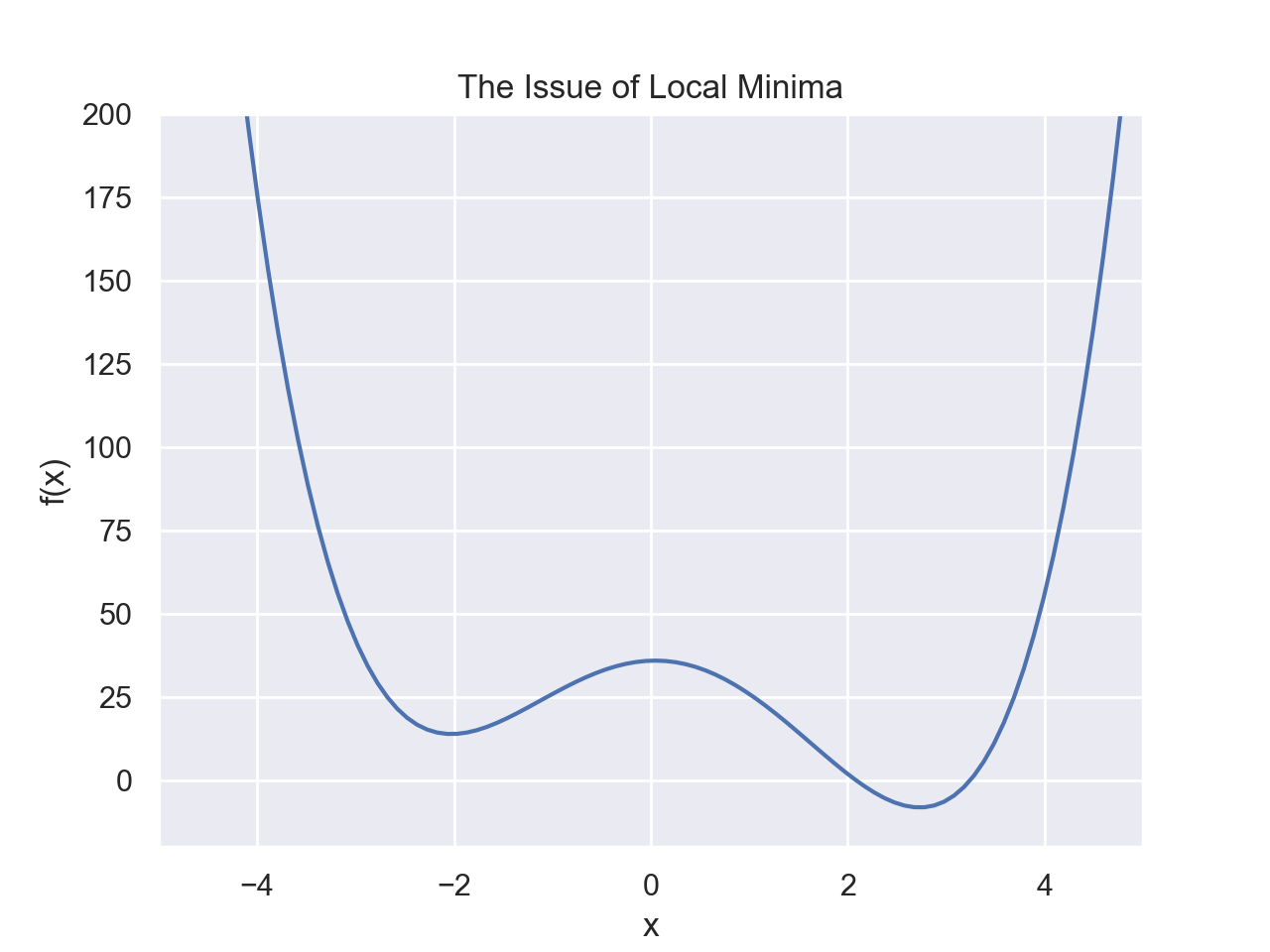

Optimization with Local Minima — Function with non-global minimum

def energy_landscape(x):
    return -(x-3)*(x+2)-10*x**2-x**3+x**4+30

x_values = np.linspace(-5,5,100)
y_values = [energy_landscape(x) for x in x_values]
plt.figure()
plt.plot(x_values,y_values)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.title("The Issue of Local Minima")
plt.xlim([-5,5])
plt.ylim([-20,200])
plt.show()

If this does not seem bad enough yet to you, consider all of the following:

This is a function of only 1 variable and the value is quick to compute if we know the function
We have a graph, so it's obvious to us since we can visually see the whole function
We have no restrictions for the value of x
The function is continuous and smooth

Optimization 2D with Local Minima — Function of 2 Variables with Many Local Minima

import numpy as np
import matplotlib.pyplot as plt

def rastrigin(x, y):
    """Compute the Rastrigin function."""
    return 20 + 0.2*x**2 + 0.1*y**2 - 2 * np.cos(0.5 * np.pi * x) - 1.5 * np.cos(0.5 * np.pi * y)

# Generate x and y data points
x = np.linspace(-5.12, 5.12, 400)
y = np.linspace(-5.12, 5.12, 400)
X, Y = np.meshgrid(x, y)
Z = rastrigin(X, Y)

# Plotting
fig = plt.figure(figsize=(14, 8))
ax = fig.add_subplot(111, projection='3d')
ax1 = ax.plot_surface(X, Y, Z, cmap='magma')
plt.colorbar(ax1)
ax.set_title("Rastrigin Function")
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Function value (Z)')
ax.view_init(45, -45)  # Adjust viewing angle for better visualization
plt.show()

Now let's imagine we are dealing with a function of 200 variables, which will take well over a thousand times longer for the computer to calculate the value of, we have constraints, and we cannot visualize the graph due to the high dimensionality. The problem has gotten immeasurably harder.

Folding Funnel

The folding funnel hypothesis frames protein folding as an optimization problem for free energy with a search space that has a steep descent with the global minimum corresponding to the native state, similar to to a funnel shape. The folding funnel permits some local minima in the landscape which correspond to misfolded states.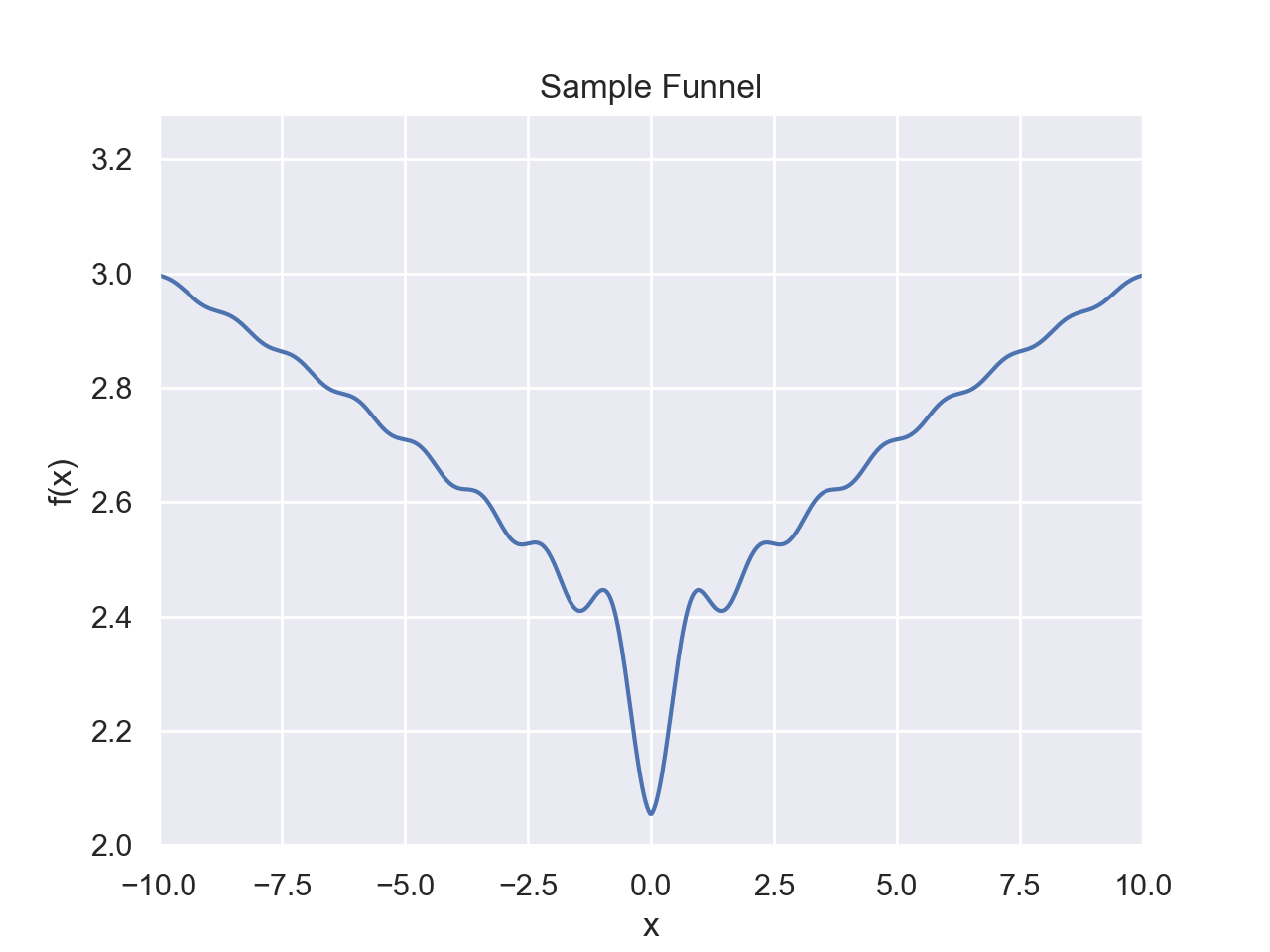

def energy_landscape(x):
    return np.log(abs(x)+10)-0.05*np.sin(5*x)/x

x_values = np.linspace(-15,15,1000)
y_values = [energy_landscape(x) for x in x_values]
plt.figure()
plt.plot(x_values,y_values)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.title("Sample Funnel")
plt.xlim([-10,10])
#plt.ylim([-20,200])
plt.show()

Assistance in Folding

Heat Shock Protein

Heat shock proteins (HSPs) are a family of proteins that are induced in response to various stress conditions, including elevated temperatures, oxidative stress, and toxic substance exposure. They play crucial roles in protein folding, maintenance of cellular protein homeostasis (proteostasis), and protection against protein aggregation, which is fundamental for cell survival under stress.

Chaperonins

Chaperonins are a subclass of molecular chaperones, essential proteins that assist in the proper folding of other proteins, preventing misfolding and aggregation. These complex structures are crucial for maintaining a healthy cellular environment and ensuring the functionality of proteins within the cell. Chaperonins undergo an ATP-dependent cycle to facilitate protein folding.

Misfolding

Prions

Prions are infectious agents comprised solely of protein, devoid of nucleic acids which are typically associated with transmission of infectious diseases. These aberrant proteins propagate by inducing misfolding in normally folded proteins of the same type, thus exemplifying an extraordinary aspect of protein folding thermodynamics. The energetic landscape of prion propagation is characterized by a multidimensional folding funnel with the native state (PrP^C) and the infectious state (PrP^Sc) residing in distinct energetic minima. The thermodynamic barrier separating these states determines the propensity for conversion and the stability of the infectious form.

Alzheimer's

Structure Determination

Evolution

Mutations

BLOSOM

BLOcks SUbstitution Matrices or BLOSOM are a way to compare sequence similarity between proteins, such as to see if they may evolutionarily related.

Applications

Heat capacity for Proteins

Heat capacity is related to the number of ways in which something can utilize energy. For example, in a monoatomic gas, there are just 3 translational degrees of freedom, each contributing \(\frac{1}{2}nR\) to the heat capacity. In a diatomic molecule, you have the energy being taken up as vibrational and rotational energy, which add to the heat capacity. You always have certain degrees where you can input energy, such as translational and rotational degrees of freedom. Once you reach a certain temperature, thermal energy can now be taken up to disrupt interactions, such as H-bonding, increasing the heat capacity. Once those molecular interactions have been broken, there are fewer ways that heat can be taken up for the protein, decreasing the heat capacity; you can't spend energy to break intermolecular forces that are already broken. Cp is still a bit higher than it was at lower temperature, however.

Differential Scanning Calorimetry

A popular experimental technique used to measure the heat capacity of proteins. This method measures the heat required to increase the protein sample's temperature compared to a reference, providing insights into heat capacity and thermal transitions.

By Schmin - Own work, Public Domain, Link

Protein Folding Exercises

How does the heat capacity of a protein relate to its denaturation?
Describe the levels of protein structure involved in folding.
How does the protonation state of amino acids affect protein structure?
Explain the concept of folding funnels.
escribe the Anfinsen experiment and its significance in understanding protein folding.
Explain the role of hydrophobic interactions in protein folding.
What are chaperone proteins and what role do they play in protein folding?
Explain the concept of the native state of a protein.